Introduction
Evoquée souvent par l’appellation « jeu de ficelle », la réalisation de figures de ficelle a pu être observée depuis la fin du 19ème siècle dans diverses aires culturelles, et tout particulièrement dans des sociétés dites de tradition orale. Dans le contexte des théories diffusionnistes de l’époque, certains anthropologues ont réalisé les premiers relevés de cette pratique dans une perspective d’ethnologie comparée. L’enjeu était alors de mettre au jour des contacts entre différentes sociétés, et les voies de migration suivies par certaines populations.
La première description technique de figures de ficelle est due à Franz Boas qui a recueilli, au début des années 1880, les méthodes de construction de deux figures « Eskimo » (Boas, 1888 : 229-230). Peu de temps après, des dessins illustrant les différentes étapes de deux jeux de ficelle connus par les Indiens Salish (Colombie-Britannique) furent publiés par l’archéologue et ethnologue Harlan I. Smith (1900). La première étude significative sur les jeux de ficelle a néanmoins été réalisée en Mélanésie par deux scientifiques de Cambridge, l’anthropologue Alfred Cort Haddon et l’anthropologue, neurologue et psychiatre William H. R. Rivers. En 1898, Rivers et Haddon ont recueilli les méthodes de construction de 31 figures de ficelle pratiquées par les insulaires du détroit de Torres (situé au nord de l’Australie), ce qui les a conduit à élaborer une nomenclature permettant d’enregistrer toutes les étapes de réalisation d’un jeu de ficelle (Rivers & Haddon, 1902, Haddon, 1912). Leur intention était d’inciter d’autres anthropologues à recueillir des jeux de ficelle dans différentes sociétés (Rivers & Haddon, 1902 : 147). Les nombreuses collections de jeux de ficelle publiées au cours du 20ème siècle en utilisant la méthode de description de Rivers et Haddon (ou des méthodes proches) montrent que cela a bien eu lieu (Gray, 1903 ; Cunnington, 1906 ; Parkinson, 1906 ; Jayne, 1906 ; Landtmann, 1914 ; Jenness, 1924 ; Hornell, 1927 ; Paterson, 1949).
Loin d’attirer l’attention des seuls ethnologues, l’activité consistant à réaliser des figures de fil a également été considérée par quelques mathématiciens comme un objet d’étude pertinent. Au début du 20ème siècle, W. W. Rouse Ball fut ainsi l’un des premiers à questionner le caractère mathématique de cette activité, qu’il identifiait comme l’un des « jeux mathématiques » particulièrement communs à de nombreuses sociétés (Ball, 1911, Vandendriessche, 2014a). Plusieurs mathématiciens, dont A. Amir-Moez (1965), T. Storer (1988), M. Yamada, R. Burdiato, H. Itoh et H. Seki (1997), ont cherché par la suite à proposer des principes de modélisation capables de rendre compte de l’organisation séquentielle de tout jeu de ficelle (Vandendriessche, 2010).
Dans les îles Trobriand de Papouasie-Nouvelle-Guinée, la pratique du jeu de ficelle a été documentée dans les années 1920 par Bronislaw Malinowski (1929 : 336-338), puis dans les années 1980 par l’ethnolinguiste Gunter Senft et son épouse Barbara Senft (1986). Comme j’ai pu le constater en menant des recherches ethnographiques dans cet archipel en 2006 et 2007, les jeux de ficelle (kaninikula) y sont encore pratiqués. Chez les Trobriandais, le jeu de ficelle est réalisé après avoir noué les extrémités d’une ficelle d’environ deux mètres — qui résulte du tressage serré de fibres extraites des racines de pandanus — pour en faire une boucle. L’activité consiste alors à appliquer une succession d’opérations sur le fil, en utilisant principalement les doigts, et parfois les poignets, la bouche ou les pieds. Cette succession d’opérations, qui est généralement réalisée par une seule personne, mais aussi parfois par deux personnes jouant ensemble, permet de déployer une figure (plane ou à 3 dimensions) entre les deux mains.
Si l’on rencontre quelques praticiens masculins trobriandais, la pratique des jeux de ficelle est présentée dans cette société comme une activité féminine ; elle est de fait pratiquée le plus souvent par des femmes et des enfants. Si les enfants jouent dans la journée, les adultes pratiquent les jeux de ficelle le plus souvent le soir, en petit groupe, réunis sur la terrasse de leur habitation sur pilotis, à la lueur d’une lampe à pétrole. Ces jeux de ficelle sont très souvent accompagnés d’un texte oral — appelé vinavina — que le praticien récite ou chante, en réalisant la figure, ou en mettant en mouvement cette dernière pour illustrer son récit. Environ un tiers des jeux de ficelle que j’ai collectés dans les îles Trobriand sont accompagnés d’un vinavina. Contrairement au terme kaninikula (cf. section 3.1), je n’ai pas encore eu accès à une interprétation du sens littéral du terme vinavina, qui ne semble utilisé que dans le contexte de la pratique des jeux de ficelle.
Les kaninikula et leur vinavina sont parfois mis en scène devant un public : ils apparaissent alors comme un divertissement théâtral qui provoque très souvent le rire dans l’assistance, en raison des connotations sexuelles et scatologiques de bon nombre d’entre eux. [1] Comme le suggère l’extrait vidéo suivant, ce sont le plus souvent les hommes qui se donnent ainsi en spectacle.
Au-delà du divertissement, ces jeux de ficelle et les textes qui les accompagnent sont dans cette société des supports de mémoire permettant de rappeler certaines règles sociales, des histoires populaires ou des évènements particuliers (Vandendriessche, 2012 et 2014c).
Dans cet article, je me concentrerai sur les aspects techniques et conceptuels de la pratique trobriandaise des jeux de ficelle, en montrant en quoi et comment la création de figures de ficelle a relevé — dans le passé — d’une activité mathématique. Je commencerai par préciser le contexte de mes recherches ethnographiques chez les Trobriandais de Papouasie-Nouvelle-Guinée, ainsi que la méthodologie mise en œuvre pour étudier les jeux de ficelle dans cette société (section 1). La section 2 proposera une analyse formelle du corpus de jeux de ficelle que j’ai ainsi recueilli, mettant au jour la manifestation d’une forme de rationalité mathématique associée à la création des figures caractéristiques de ces jeux. Je montrerai ensuite (section 3) comment certaines données linguistiques — relatives à la pratique contemporaine des jeux de ficelle dans les îles Trobriand — nous renseignent sur la façon dont des praticiens perçoivent et conceptualisent aujourd’hui cette pratique. Croiser ces observations avec les résultats de l’analyse formelle des jeux de ficelle trobriandais permet d’éclairer les processus de création qui ont été à l’œuvre dans l’élaboration des procédures de jeu de ficelle.
1. Contextes du recueil de jeux de ficelle contemporains dans les îles Trobriand
Les îles Trobriand forment un archipel d’atolls coralliens d’une superficie totale d’environ 440 km². Situé au large de la pointe Sud-Est de la grande terre de Papouasie-Nouvelle-Guinée, il est composé de l’île principale, Kiriwina — sur laquelle vit une grande partie des 20 000 habitants de cet archipel — et trois autres îles plus petites, Vakuta, Kaile’una et Kitava, auxquelles s’ajoutent quelques îlots inhabités ou peuplés seulement de quelques familles.
Dans cette région, le climat est tropical avec deux saisons principales : la saison des pluies de décembre à avril et la saison sèche de mai à novembre. Pendant la saison sèche, les Trobriandais se consacrent presque exclusivement à la culture des jardins, et produisent ainsi les légumes et tubercules — ignames, taros, manioc, patates douces, et certains légumes verts — qui, associés à la pêche et à un peu d’élevage de porcs et de volailles, offrent l’essentiel de leurs moyens de subsistance. Par contraste, la saison des pluies est une période qui interdit tout travail dans les jardins. Cette saison est privilégiée pour mener d’autres activités telles que la sculpture sur bois, le tressage de nattes, ou encore les jeux de ficelle.
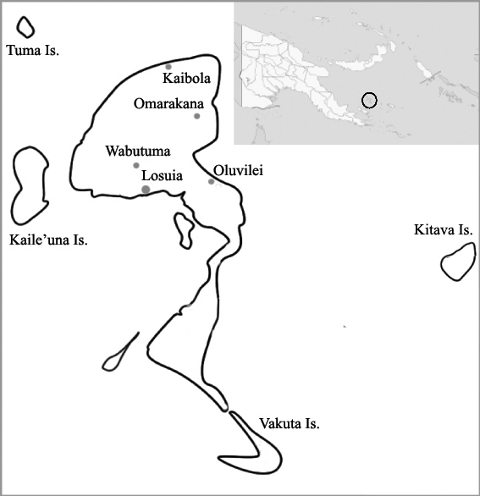
Mon enquête ethnographique a été menée principalement dans le village d’Oluvilei, situé sur la côte orientale de Kiriwina, à environ 10 km de Losuia, le village principal de l’île. J’ai par la suite élargi mes recherches à d’autres villages de l’archipel : Kaibola (sud de Kiriwina), Wabutuma (centre de Kiriwina), et Kaulaka (îlot Vakuta) en particulier.
Dans cette société — tout comme dans les autres sociétés où j’ai enquêté — je n’ai pas assisté à des créations de nouvelles figures de ficelle, mais j’ai pu travailler avec des praticiens que je qualifie d’« experts », possédant des compétences reconnues par les autres membres de la communauté pour la réalisation de figures de fil. Ces experts connaissent la plupart des jeux de ficelle pratiqués dans le village et sont capables de les réaliser lentement, étape par étape, pour en faciliter l’apprentissage par autrui [2]. À Oluvilei, trois femmes (deux d’une quarantaine d’années et la troisième d’une soixantaine d’années) sont reconnues comme des expertes de cette activité. Ce travail entrepris avec ces experts m’a permis de constituer un corpus composé de 58 jeux de ficelle, qui a été augmenté par la suite de 17 jeux de ficelle grâce à des enquêtes menées au-delà d’Oluvilei. C’est sur ce corpus de 75 jeux de ficelle — désigné ci-dessous par Corpus trobriandais — que porte mon analyse.
J’ai commenté ailleurs la méthode mise au point par Rivers et Haddon pour enregistrer les étapes de réalisation d’une figure de ficelle (Vandendriessche, 2007). Cette méthode d’enregistrement a par la suite fait l’objet de diverses améliorations au cours du 20ème siècle. En particulier, les membres de l’association ISFA [3] (International String Figure Association) ont mis au point une manière synthétique de noter les séquences opératoires des jeux de ficelle : j’en propose ici une adaptation en français. Celle-ci est détaillée sur la page de nomenclature du document web qui rassemble les descriptions des jeux de ficelle (lien vers le sommaire de ce document) présentés dans la suite de cet article.
2. Aspects mathématiques des jeux de ficelle trobriandais
L’introduction dans cette section de quelques outils conceptuels (opération élémentaire, sous-procédure, sous-procédure itérative, ouverture, etc.) va permettre de faire des hypothèses sur les opérations mentales à caractère mathématique qui ont sous-tendu la création des jeux de ficelle trobriandais dans le passé.
2.1 Opérations élémentaires
Un jeu de ficelle peut toujours se décrire par une succession de « gestes simples », que je qualifie d’« opérations élémentaires » dans le sens où tout jeu d’un même corpus peut être décrit en invoquant un certain nombre d’entre elles. Je propose donc de regarder un jeu de ficelle comme une « procédure » (ou comme un « algorithme ») composée d’une succession d’opérations élémentaires (Vandendriessche, 2007 et 2010). La plupart de ces opérations peuvent être définies comme des opérations « géométriques » qui ont pour finalité de modifier une configuration donnée en une autre. Quelques opérations n’engendrent quant à elles aucune modification de la configuration de fil, décrivant simplement le mouvement d’un doigt autour ou à travers cette configuration (voir plus loin les opérations « passer » et « insérer »). Dans le cas du corpus trobriandais, nous pouvons identifier treize opérations élémentaires ayant une action directe sur le fil. Le lecteur en trouvera la liste ci-dessous, chacune de ces opérations étant illustrée par un court extrait vidéo.
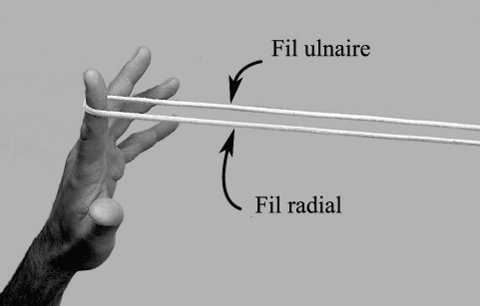
La ficelle passant autour d’un doigt forme une « boucle » (Fig. 2a). Une boucle est alors composée de deux « fils » : un fil « radial » (côté du pouce) — un fil « ulnaire » (côté de l’auriculaire). En employant les noms des cinq doigts de la main, les termes « radial » et « ulnaire », gauche et droite, il devient alors possible de désigner chacun des vingt fils qui peuvent être créés entre les deux mains. Par exemple, la figure 2a montre les fils ulnaire et radial de l’index gauche.
Deux boucles sont parfois formées sur un même doigt : l’une est alors qualifiée de boucle « distale » (côté du bout du doigt) et l’autre de boucle « proximale » (côté du poignet) (Fig. 2b).
Les termes « radial », « ulnaire » (« ulnar » en anglais), « distal », « proximal », ainsi que « dorsal » (côté de la face dorsale de la main) et « palmaire » (« palmar » en anglais — côté de la paume) sont les six adjectifs de spatialisation introduits par Rivers et Haddon qui permettent de définir précisément les différentes parties du fil sur lesquels les doigts — et parfois les dents ou les pieds — opèrent (Rivers & Haddon 1902).
Opérations de saisie d’un fil
On peut distinguer six opérations élémentaires dont la finalité est de saisir un (ou plusieurs) fil(s) :
- « saisir » un fil avec la face dorsale du doigt
- « crocheter (le fil) vers le haut » (avec la face palmaire du doigt)
- « crocheter (le fil) vers le bas » (avec la face palmaire d’un ou plusieurs doigts)
- « pincer » (le fil) entre les dents
- « attraper » (le fil) entre deux doigts
- « prendre » plusieurs fils à la fois avec plusieurs doigts (ou la bouche)
Après la saisie d’un fil avec un doigt (« saisir », « crocheter »), ce dernier peut, suivant les cas, reprendre ou non sa position initiale. Le retour possible à la position de départ peut être analysé comme une opération élémentaire que nous désignerons par l’expression « revenir en position ».
Opération de tension du fil
Après une série d’opérations, le fil est généralement tendu entre les deux mains :
- « tendre » le fil
Opération de libération d’une boucle
Un doigt peut libérer la boucle qu’il porte. Cette opération a généralement pour effet de modifier profondément la configuration de fil, provoquant la déconstruction d’une partie de celle-ci :
- « libérer » une boucle
Opérations de rotation
On peut distinguer trois types de rotation : les deux rotations « verticale » et « horizontale » qu’effectuent les mains, et la rotation d’un doigt portant une boucle qui a pour effet de « torsader » cette dernière :
- « rotation verticale » de la main
Une telle rotation est exécutée suivant les cas en tournant la paume vers l’extérieur ou l’intérieur du corps.
- « rotation horizontale » de la main
Une rotation horizontale peut également être exécutée dans deux sens différents : dans le sens horaire ou inverse horaire (pour un observateur que nous choisirons situé sur la gauche du praticien).
- « torsader » (une boucle)
Opération d’élargissement
Cette opération permet d’ « élargir » une partie de la configuration en insérant simultanément et symétriquement deux doigts dans un espace circonscrit par certains fils de la figure [4] :
- « élargir »
Terminons l’inventaire des opérations élémentaires par deux opérations sans action directe sur le fil qui sont mises en œuvre dans certains jeux de ficelle trobriandais.
Opérations d’insertion et de passage
Un doigt de la main ou du pied est parfois « inséré » dans une boucle par le côté distal ou par le côté proximal :
- « insérer » un doigt dans une boucle
Un doigt, une main, la bouche ou un pied doivent parfois « passer » par le côté distal ou proximal d’un fil ou d’une boucle.
- « passer » par le côté distal/par le côté proximal d’un fil ou d’une boucle
Montrons à présent comment ces opérations s’organisent en procédures en décrivant un premier jeu de ficelle trobriandais. Le lecteur est invité à ce stade de l’article à se munir d’un fil d’environ deux mètres de long, de le nouer sous forme de boucle, et de réaliser les figures de ficelle auxquelles nous ferons référence. Pour simplifier la description des jeux de ficelle, les doigts seront numérotés de 1 à 5 du pouce à l’auriculaire. Les côtés « droit » et « gauche » seront indiqués par les abréviations D et G. Par exemple, le pouce de la main droite sera noté D1, la boucle portée par ce doigt sera désignée par l’expression « boucle D1 », et enfin, le fil radial et le fil ulnaire de la boucle D1 seront respectivement désignés par « fil D1 radial » et « fil D1 ulnaire ». Lorsque la mention D ou G est omise, cela signifie que les deux doigts homologues opèrent symétriquement [5].
La procédure kapiwa (abeille) débute par une série d’opérations que Rivers et Haddon proposèrent d’appeler « Ouverture A » (voir section 2.2 et Ouverture A).
1. « Ouverture A »
2. « Insérer » 2345 dans les boucles 1 par le côté distal. « Prendre » avec 2345 les fils 1 ulnaires et les boucles 2 et 5. Effectuer une « rotation horizontale » de la main gauche dans le sens inverse horaire. « Libérer » la boucle G1 dans le mouvement (le fil G1 radial passe sur la face dorsale des mains). Faire les mêmes opérations avec la main droite. « Revenir en position » (main face à face).
3. « Saisir » les fils 2 radiaux avec les pouces (les boucles qui étaient initialement sur les pouces sont ainsi transférées aux poignets).
4. « Passer » 1 par le côté proximal des boucles des poignets. « Insérer » 1 dans les boucles 5 par le côté proximal. « Saisir » les fils 5 ulnaires et « revenir en position ». « Libérer » 5.
5. « Insérer » 5 dans les boucles 2 par le côté proximal. « Libérer » 2.
6. « Insérer » 1 par le côté proximal dans les boucles 5. « Saisir » avec 1 les fils 5 radiaux et « revenir en position ».
7. « Insérer » 2 par le côté proximal dans les boucles 1 ulnaires. « Saisir » avec 2 les fils 1 ulnaires. « Libérer » 5 puis 1 en effectuant une « rotation verticale » des mains (paumes vers l’extérieur).
(voir également la page web kapiwa)
Dans cette procédure, les opérations élémentaires sont effectuées de façon symétrique par les deux mains, ce qui conduit à une figure symétrique par rapport à un axe vertical parallèle aux mains. Bien qu’il y ait quelques exceptions [6], ce principe de symétrie est un trait caractéristique du corpus, et plus généralement des corpus océaniens que j’ai étudiés (Jenness, 1920 ; Rosser & Hornell, 1932 ; Davidson, 1941 ; Maude, 1978 ; Noble, 1979). Ces corpus se différencient notamment des corpus de l’Arctique dans lesquels de nombreux jeux de ficelle sont réalisés de façon asymétrique (Jenness, 1924 ; Victor, 1940 ; Paterson, 1949 ; Mary-Rousselière, 1969). L’analyse comparative que j’ai menée précédemment à partir du corpus de jeux de ficelle collectés dans des sociétés culturellement contrastées suggère de plus que les opérations élémentaires sont généralement les mêmes d’un corpus à l’autre. Néanmoins, j’ai pu noter que les fréquences d’utilisation de certaines de ces opérations peuvent varier significativement d’une société à l’autre (Vandendriessche, 2010 et 2014b).
La détermination des opérations élémentaires a résulté d’une analyse formelle du corpus trobriandais, et d’un « séquençage » des procédures de jeu de ficelle en « éléments simples », ce qui permet la description et l’analyse de tout jeu de ficelle du corpus. Même si cette conceptualisation fait écho à une terminologie vernaculaire désignant certaines actions exécutées lors de la pratique des jeux de ficelle dans les îles Trobriand (section 3.3), il s’agit bien sûr ici d’un point de vue d’observateur. Néanmoins, comme nous allons le voir dans les sections suivantes, l’organisation de ces opérations en « sous-procédures », ainsi que la mise au jour de certaines procédures qui diffèrent d’une et une seule opération, renvoient à la façon dont des créateurs de jeux de ficelle ont pu explorer les possibilités combinatoires de ces algorithmes.
2.2 Modification ou ajout d’une et une seule opération élémentaire
Dans le corpus trobriandais, on peut identifier des couples de jeux de ficelle tout à fait singuliers, les deux procédures étant identiques à une opération élémentaire près. Deux cas se présentent alors : 1) une opération élémentaire a été substituée à une autre ; 2) une (et une seule) opération a été ajoutée (ou supprimée) au sein d’une procédure donnée. Les jeux de ficelle tobutu topola (pêcheurs rabattant les poissons / pêcheurs tenant le filet) [7] et tosalilagelu (personne sculptant un canot) illustrent la première situation. Le document tobututopola-tosalilagelu met en évidence que les procédures diffèrent par une opération appliquée à l’étape 3. En effet, l’opération d’insertion des annulaires dans la boucle des auriculaires se fait par le côté distal (par le dessus) dans la procédure tobutu topola, et par le côté proximal (par le dessous) dans la procédure tosalilagelu. Cette variation opératoire a pour conséquence de modifier la figure finale de façon significative (figures ci-dessous [8]).
Les jeux de ficelle kenabosu (bâtonnet taillé dans une arête du poisson bosu), vivilua (nom d’une personne), et samula kayaula (nom d’une rivière), illustrent le second type de modification opératoire mentionné plus haut. Ces trois procédures sont présentées en parallèle dans le document vivilua-kenabosu-samulakayaula. La procédure kenabosu débute par l’ouverture A (cf. jeu de ficelle kapiwa décrit plus haut) suivie d’une sous-procédure que nous appellerons K pour les besoins de l’analyse. La procédure vivilua débute également par l’ouverture A. L’opération élémentaire « torsader » (une boucle) est alors appliquée à la boucle des index, suivie de la sous-procédure K. On passe donc de la procédure kenabosu à vivilua, et réciproquement, par ajout ou suppression d’une et une seule opération élémentaire. De même, il suffit d’itérer l’opération « torsader » (une boucle) de la procédure vivilua, et d’appliquer ensuite de la même façon la sous-procédure K, pour obtenir le jeu de ficelle samula kayaula.
Les deux cas de modification opératoire que nous venons d’analyser — et les très nombreux exemples de ce type que contient le corpus trobriandais — tendent à confirmer que des acteurs ont modifié, ajouté ou supprimé, une ou plusieurs opérations de certaines procédures, créant ainsi de nouveaux jeux de ficelle qui ont été intégrés au corpus. Ces modifications opératoires ont-elles été menées « intentionnellement », dans le but d’en mesurer les conséquences topologiques sur le jeu de ficelle ? Difficile à dire à partir de ces matériaux. Quoiqu’il en soit, même si ces modifications ont eu lieu « accidentellement » au cours d’un jeu de ficelle, le praticien aura su identifier l’opération modifiée par erreur au sein de la procédure. Que ces variations opératoires aient eu lieu par accident ou intentionnellement, elles témoignent dans les deux cas du haut degré d’expertise de ces praticiens.
2.3 Le concept de sous-procédure
De façon remarquable, on peut identifier dans les algorithmes de jeu de ficelle des séquences ordonnées d’opérations élémentaires — que j’appelle des « sous-procédures » — se retrouvant à l’identique dans plusieurs jeux de ficelle, ou itérées au sein de la même procédure. De nombreuses sous-procédures sont impliquées dans le corpus trobriandais. Sans en faire une liste exhaustive, décrivons ici quelques exemples de sous-procédures communes à plusieurs jeux de ficelle du corpus.
2.3.1 Ouvertures
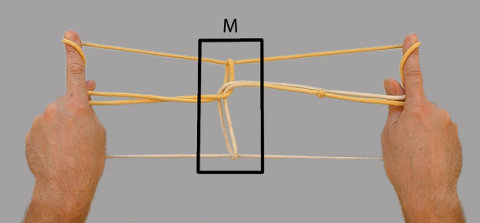
Une famille singulière de sous-procédures est celle des « ouvertures » (ou « openings » en anglais) : ce terme, introduit par Rivers et Haddon (1902), désigne une série d’opérations de démarrage qui initie la procédure de jeu de ficelle par la création de boucles sur certains doigts. L’ouverture A introduite plus haut est impliquée dans 42 jeux de ficelle du corpus trobriandais. Cette courte série d’opérations peut ainsi être analysée comme une sous-procédure. Cette dernière débute par la position initiale appelée « Position I » par Rivers et Haddon, puis les deux fils palmaires sont « saisis » tour à tour et le fil « tendu » (voir Ouverture A et l’étape 1 du jeu de ficelle kapiwa décrit dans la section 2.1). Le corpus trobriandais contient deux ouvertures principales, l’ouverture A, et l’ouverture que l’on rencontre dans certaines publications antérieures sous l’appellation « Murray Opening » (Maude, 1978 ; Noble, 1979), et que je note « ouverture M » [9] (voir Ouverture M). Cette ouverture compte 8 occurrences dans le corpus :
J’ai pu dénombrer quinze ouvertures différentes dans le corpus trobriandais (Vandendriessche, 2010). Néanmoins, seulement quatre d’entre elles sont impliquées dans au moins deux jeux de ficelle du corpus, et peuvent ainsi être analysées comme des sous-procédures [10].
2.3.2 Courtes sous-procédures
Certaines sous-procédures — que j’appelle « courtes sous-procédures » — sont constituées d’un petit nombre d’opérations élémentaires, et sont impliquées avec une grande fréquence dans le corpus. L’étape 5 du jeu de ficelle kapiwa décrit plus haut en est un exemple. Il s’agit d’une sous-procédure qui permet de transférer une boucle portée par un doigt à un autre doigt de la même main. Cette courte sous-procédure — que je désigne par l’expression « transfert d’une boucle » — consiste en deux opérations élémentaires successives : une insertion suivie d’une libération :
Deux autres courtes sous-procédures ont également une grande occurrence dans le corpus : il s’agit de deux opérations déjà identifiées dans certains relevés ethnographiques sous l’appellation « Navaho » [11] et « Caroline extension » [12]. Lorsque deux boucles sont portées par un même doigt, la sous-procédure Navaho consiste à « saisir » (avec les dents ou avec l’index et le pouce) le fil radial de la boucle proximale, pour le faire « passer » par-dessus la boucle distale, puis par-dessus l’extrémité du doigt avant de le « libérer », comme illustré sur le document Navaho et le court extrait vidéo suivant :
Lorsqu’une boucle est formée sur le pouce, la sous-procédure « Caroline extension » consiste à :
1. « Insérer » 2 dans la boucle 1 par le côté proximal.
2. « Saisir » avec 2 le fil 1 ulnaire tout en « attrapant » (ou pressant) ce fil entre 1 et 2.
3. Effectuer avec la main une « rotation verticale ».
Nous reviendrons plus loin sur ces deux sous-procédures (Navaho et Caroline extension) que désignent deux termes vernaculaires (section 3.3). Donnons à présent un exemple d’une sous-procédure plus longue.
2.3.3 Autres sous-procédures
La mise en œuvre de la sous-procédure « Caroline extension » est très souvent précédée (mais pas systématiquement) d’une même séquence d’opérations élémentaires (étapes 1 et 2 ci-dessous). Cette séquence suivie de la « Caroline extension » forme ainsi une sous-procédure (que nous noterons « sous-procédure E » dans la suite) qui peut se décrire ainsi :
1. « Passer » 1 par le côté distal de la boucle 2.
2. « Saisir » avec 1 le fil 5 radial et « revenir » en position.
3. Caroline extension.
Cette sous-procédure est très souvent utilisée dans le corpus trobriandais pour « déployer » la figure finale d’un jeu de ficelle. L’expression « Caroline extension » utilisée dans la littérature ethnographique sur les jeux de ficelle semble du reste renvoyer à ce phénomène. Les séquences vidéo suivantes illustrent l’ « extension » de deux figures finales du corpus sous l’action de la sous-procédure E décrite ci-dessus :
Le lecteur trouvera le détail de ces deux procédures dans les documents kalatugebinavalulu et misima. Notons que la sous-procédure E est parfois utilisée pour une autre étape que l’extension finale. Par exemple, dans la procédure meta (piège), la sous-procédure E (meta : étape 2) est suivie de la courte sous-procédure « Navaho », de la libération d’une boucle et d’une rotation verticale qui conclut le jeu de ficelle (meta : étape 3) ; phénomène illustré par l’extrait vidéo suivant :
Comme mentionné plus haut, certaines sous-procédures sont d’un type très particulier. Il s’agit de sous-procédures — que j’appelle « sous-procédures itératives » — qui sont itérées au sein de la même procédure de jeu de ficelle. La forte occurrence de ces sous-procédures singulières dans le corpus trobriandais est d’une grande importance pour notre analyse. En effet, ce phénomène tend à confirmer que la recherche de sous-procédures itératives a guidé les créateurs de jeux de ficelle dans leurs investigations sur ces algorithmes.
2.4 Le concept d’itération
J’ai défini ailleurs ce que j’appelle le « dessin » d’une figure finale, comme étant la forme géométrique que l’on peut extraire de cette figure sans tenir compte du trajet exact du fil (Vandendriessche, 2007). Certains dessins du corpus de jeux de ficelle trobriandais semblent avoir été conçus par la répétition d’un même « motif » simple. Dans certains cas, c’est l’itération d’une sous-procédure qui entraîne la répétition d’un motif donné. Deux cas se présentent alors : dans le premier cas, la sous-procédure itérative est répétée autant de fois que la longueur du fil le permet, le même motif étant créé et montré à chaque itération. La procédure budi budi (nom d’une île de la province de Milne Bay, Papouasie-Nouvelle-Guinée - budi budi) est élaborée autour d’une sous-procédure itérative de ce type :
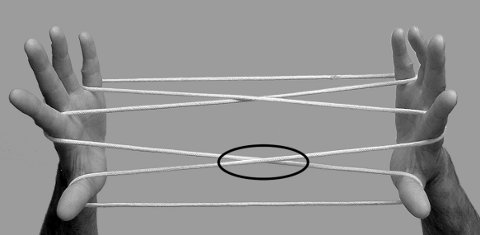
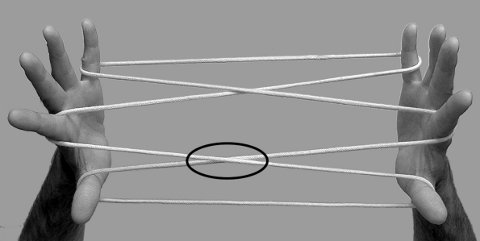
Dans le second cas, la sous-procédure itérative n’est réalisée qu’un nombre précis de fois. C’est le cas en particulier de la procédure vivi (noix, dont j’ai manqué l’identification - vivi). Dans ce jeu de ficelle, la sous-procédure doit être itérée « exactement trois fois » pour faire apparaître en ligne trois motifs que j’appelle des « losanges à double côté » — motif que l’on a rencontré plus haut au centre de la figure kapiwa (Section 2.1) ; si l’on itère cette sous-procédure deux ou quatre fois, on aboutit à une configuration qui ne se déploie pas sous l’action d’une « Caroline extension ». Notons enfin que contrairement à la procédure budi budi, les trois motifs n’apparaissent qu’à la fin de la procédure, sous l’effet de l’extension finale :
Par contraste avec la situation précédente, l’impact de certaines sous-procédures itératives sur la figure finale est parfois plus difficile à percevoir. C’est le cas de la sous-procédure qui est itérée au sein du jeu de ficelle salibu (miroir - salibu). Après l’ouverture A, les deux étapes suivantes (salibu : étapes 2 et 3) permettent de mettre le fil dans une configuration — que j’appelle Conf(B) [13] — sur laquelle va être implémentée la sous-procédure en question, que je nomme ici « sous-procédure S ».

La sous-procédure itérative S appliquée une première fois à Conf(B) peut se résumer par la série d’opérations suivante (voir également salibu : étape 4) :
« Passer » 1 par le côté proximal des boucles de 2, « saisir » le fil radial de 5, et « revenir en position » :
« Insérer » 1 dans la boucle distale de 2, « saisir » le fil 2 radial et « revenir en position » :
Navaho 1 :
La libération de la boucle distale des index et le transfert de la boucle des pouces aux index permet de replacer le fil dans une configuration « proche » de Conf (B) (Fig. 6), dans le sens où elle consiste également en deux boucles sur chaque index, et une boucle sur chaque auriculaire (salibu : étape 5) :

La sous-procédure S décrite plus haut est alors itérée (voir également salibu : étape 6) :
et enfin quelques opérations suffisent à déployer la figure :
À l’issue de cette itération, il est théoriquement possible de mener une seconde itération de la sous-procédure S. Il faut pour cela remettre le fil dans une configuration « proche » de Conf(B), en procédant de la même façon qu’entre la première occurrence de la sous-procédure S et sa première itération (libération de la boucle 2 distale et transfert de la boucle 1 à 2 : salibu : étape 5). Cette possibilité ne semble pas avoir été envisagée dans les îles Trobriand. En revanche, elle a été enregistrée par les anthropologues James Hornell et W.E. Rosser dans les années 1930 en Nouvelle-Guinée britannique, sous le nom de bava (Crabe) (Rosser et Hornell 1932).
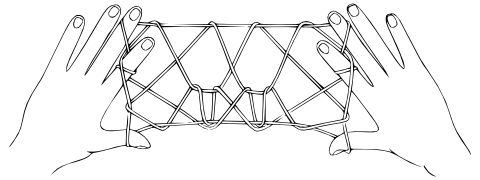
Des itérations successives de cette sous-procédure S peuvent être menées autant de fois que la longueur du fil le permet. Néanmoins, je n’ai noté, ni dans la littérature ethnographique, ni dans mes propres relevés, de procédures qui témoigneraient d’un tel phénomène.
Terminons cette section par un autre exemple singulier. Il s’agit de la procédure totuwana kalaniya kuliyava (os de dauphin - totuwana, voir également la première vidéo de cet article) qui donne à voir l’itération d’une très longue sous-procédure. La procédure débute par l’ouverture A, qui est suivie d’une longue séquence d’opérations — que nous appellerons sous-procédure T (totuwana : étapes 2 à 8) — menant à une première figure intermédiaire (Fig. 9a), et transformée par quelques opérations en une seconde figure intermédiaire (Fig. 9b).
Cette dernière figure de fil est alors déposée sur le sol et saisie comme le montre le court extrait vidéo suivant (voir également totuwana : étape 9) :
On obtient ainsi une configuration — que j’appelle A* — qui, bien que très proche de celle obtenue après l’ouverture A, diffère de celle-ci sur l’un des deux croisements (simples) du fil (Fig. 9a et 9b).
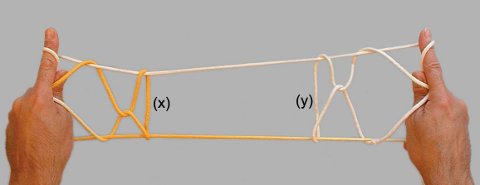
La sous-procédure T est ensuite itérée pour obtenir la figure finale du jeu de ficelle (Fig. 10b).
Cette dernière figure est très proche de la figure intermédiaire obtenue à l’issue de la première implémentation de la sous-procédure T (Fig. 10a) : en effet, tout se passe comme si les deux brins (x) et (y) de cette figure intermédiaire avaient été coupés et entrelacés. Ce phénomène résulte clairement de la modification de la configuration de départ (configuration A*) sur laquelle est opérée l’itération de la sous-procédure T.
L’itération d’un motif ou d’une sous-procédure est à l’œuvre dans de nombreux corpus de jeux de ficelle. Néanmoins, il semble que l’usage de l’itération soit un trait distinctif d’un corpus à l’autre : dans le corpus de jeux de ficelle que j’ai recueilli chez les Guarani-Ñandeva du Chaco paraguayen (Vandendriessche, 2010, 2014a et 2014b), mais aussi dans les corpus de l’Arctique (Jenness, 1924 ; Victor, 1940 ; Mary-Rousselière, 1960), ce procédé n’est que rarement utilisé, alors qu’il est constant dans le corpus des îles Trobriand et plus généralement dans ceux du Pacifique que j’ai étudiés (Hornell, 1927 ; Maude, 1978 ; Noble, 1979).
Les nombreuses sous-procédures impliquées dans le corpus trobriandais témoignent d’un travail intellectuel qui a été mené par les acteurs pour créer de nouveaux jeux de ficelle. Ce travail a vraisemblablement consisté à identifier des ensembles ordonnés d’opérations — les sous-procédures — ayant une action différentielle sur des substrats différents (positions particulières du fil). De plus, nous l’avons vu plus haut, l’analyse de certains jeux de ficelle suggère que des praticiens ont exploré ces algorithmes en appliquant des principes opératoires tels que ceux de « variation opératoire » (modification ou ajout d’une et une seule opération élémentaire) ou d’ « itération » (sous-procédure itérative). Tournons-nous à présent vers un autre concept impliqué dans de nombreux corpus de jeux de ficelle : le concept de transformation.
2.5 Transformation
Dans tous les corpus de jeux de ficelle que j’ai étudiés (et le corpus trobriandais en particulier), le concept de transformation est à l’œuvre à plusieurs niveaux. D’une part, ce concept est omniprésent puisqu’une figure de fil est le résultat de la transformation continue d’une boucle de ficelle. D’autre part, certains exemples (comme celui de budi budi de la section précédente) suggèrent que des praticiens ont cherché à transformer la « géométrie » de certaines figures finales en ajoutant ou en supprimant un « motif » donné, par itération d’une sous-procédure notamment. Enfin, d’autres exemples étayent l’hypothèse que des praticiens ont cherché à transformer une figure donnée en une autre figure du corpus.
2.5.1 Transformer la géométrie des figures finales
Dans des travaux antérieurs, j’ai montré que des praticiens (des îles Salomon notamment) ont exploré les combinaisons possibles de quelques motifs simples pour créer de nouveaux dessins de figure finale (Vandendriessche, 2007 : 69-72). Même si ce phénomène semble moins impliqué dans le corpus trobriandais que dans celui des îles Salomon publié par Honor Maude (1978), certains exemples tendent à montrer que de telles investigations ont également été menées par les praticiens trobriandais. La figure finale de la procédure tokopokutu (peigne à poux — tokopokutu) est composée d’un seul motif que nous noterons ici M dans la suite (Fig. 11a).
Ce motif M apparaît dans plusieurs figures du corpus : la figure finale du jeu de ficelle tobutu topola est composée de quatre motifs M placés en ligne, alors que celle du jeu tosalilagelu contient deux motifs M aux extrémités de la figure (tobututopola-tosalilagelu - voir plus haut Fig. 3b et 3d). Enfin, l’une des figures intermédiaires du jeu de ficelle katala lasi - katala buwa (deux variétés de noix de bétel), est composée de deux motifs M en ligne (Fig. 11b). Ce motif a par ailleurs été combiné au « losange à double côté » du jeu de ficelle kapiwa, comme le montre la figure finale de la procédure guyau-bolu-guyavila (chef-coupe-femme du chef - guyau-bolu-guyavila) (Fig. 12).
Ces exemples, comme d’autres, tendent à montrer que des praticiens trobriandais ont parfois exploré les algorithmes de jeux de ficelle avec pour objectif de transformer la géométrie des dessins de certaines figures finales, par l’accumulation ou l’effacement de quelques motifs singuliers. Un autre mode d’investigation a très certainement consisté à chercher un « chemin » pour transformer une figure de fil donnée en une autre figure connue par ailleurs.
2.5.2 Transformation d’une figure en une autre
La longue procédure mwaya tomdawaya (Tomdawaya traverse la rivière — mwaya tomdawaya) débute par une telle transformation. Dans un premier temps, cette procédure se déroule comme celle du jeu de ficelle salibu (miroir — Section 2.3), hormis le fait que la figure est ici présentée les paumes orientées vers le haut, alors que la figure salibu est ouverte par une rotation verticale des mains qui oriente les paumes vers l’extérieur (Fig. 13a et 13b).
Ensuite, cette figure est transformée en une autre figure composée de quatre « losanges en ligne ». Le dessin de cette figure est celui de plusieurs figures finales du corpus. En particulier, on le retrouve dans le jeu de ficelle kalatugebi navalulu (linge/couche en tissu coiffant une femme venant d’accoucher - kalatugebinavalulu). De façon remarquable, la figure composée de quatre « losanges » obtenue par la transformation de salibu dans la procédure mwaya tomdawaya est identique (à un retournement près) à celle de kalatugebi navalulu [14].
Ce phénomène m’a incité à analyser ces procédures de façon plus approfondie. Dans mes travaux antérieurs, j’ai conduit cette analyse en utilisant et en développant l’outil mathématique appelé « heart-sequence » — que je traduis par « séquence essentielle » — mis au point il y a quelques décennies par le mathématicien américain d’origine navaho Thomas Storer (1988). Le principe est de focaliser l’attention sur le mouvement des « boucles » pendant le déroulement du jeu de ficelle, sans prendre en compte la façon dont les doigts opèrent sur le fil. En rendant compte des mouvements de boucles au cours du processus, et en les traduisant par une formule de type mathématique, la séquence essentielle donne — ce que j’ai proposé d’appeler — un point de vue « topologique » sur les algorithmes de jeu de ficelle (Vandendriessche, 2014b et 2014d).
Storer a montré qu’un jeu de ficelle peut être résumé en un certain nombre d’insertions d’une boucle dans une autre. En numérotant les doigts de 1 à 5 du pouce à l’auriculaire, et en notant i∞ la boucle portée par le ième doigt, on peut rendre compte formellement de ces insertions.
Les photos ci-dessus (Fig. 15) montrent une série d’opérations dont le but est de faire passer par le dessus la boucle initialement portée par le pouce (noire, notée 1∞) à l’intérieur de la boucle portée par l’index (jaune, notée 2∞). Formellement, cette insertion est notée , les flèches indiquant le mouvement de la boucle 1∞ puis son insertion dans la boucle 2∞. Finalement, la boucle noire (1∞) est transférée au majeur (doigt 3), ce qui est noté . On obtient ainsi la séquence [15] :
Par analogie avec la pratique d’un instrument de musique, j’ai proposé ailleurs de regarder un jeu de ficelle comme une séquence essentielle à laquelle est associé un certain « doigté » [16]. La séquence essentielle devient alors la « partition » à interpréter avec un doigté adapté qui n’est pas unique (Vandendriessche, 2014b et 2014d).
L’analyse de la transformation de la figure salibu en la figure de kalatugebi navalulu nécessite un trop long développement (mathématique) pour être exposé dans cet article (Vandendriessche, 2014b). Néanmoins, retenons ce que cette démonstration suggère quant aux méthodes imaginées par les créateurs de ces jeux de ficelle pour transformer une figure en une autre. Appelons S et K les algorithmes menant aux figures salibu et kalatugebi navalulu respectivement. L’analyse des séquences essentielles de ces deux algorithmes montrent que la procédure de transformation de salibu en quatre losanges consiste, dans un premier temps, à parcourir l’algorithme S à l’envers, en déconstruisant la figure salibu. Cette déconstruction permet de retrouver une configuration obtenue au cours de l’algorithme K ; configuration qui apparaît comme un point de « bifurcation » à partir duquel la partie restante de la séquence essentielle de l’algorithme K peut être implémentée, permettant ainsi l’obtention des quatre losanges. Notons que dans le jeu de ficelle mwaya tomdawaya, la réalisation de cette partie de la séquence essentielle de l’algorithme K se fait avec un « doigté » très différent de celui effectivement mis en œuvre dans l’algorithme K (mwaya tomdawaya et kalatugebinavalulu).
Cet exemple est d’une importance primordiale pour notre analyse ethnomathématique. La connexion de ces deux algorithmes au niveau des séquences essentielles tend à confirmer que les créateurs de ces procédures en avaient une connaissance à un niveau que je qualifie de « topologique » — i.e. au niveau des mouvements du fil et des insertions de boucles engendrés par la procédure. Ils ont pu ainsi connecter des algorithmes entre eux en identifiant des points de rencontre potentiels permettant des bifurcations.
2.6 Différents chemins pour la même figure
Outre la mise en œuvre de la transformation d’une figure en une autre, l’exemple précédent suggère que des procédures de jeu de ficelle auraient parfois été créées dans le but de trouver plusieurs « chemins » menant à des figures finales très proches. Dans cet exemple, on a affaire à deux procédures menant à deux figures identiques (à une rotation près). Dans d’autres cas, c’est le même dessin qui a été recherché par l’élaboration de procédures différentes. Par exemple, le dessin de la figure finale de kalatugebi navalulu (quatre losanges en ligne) est le même que celui de la procédure udi (banane - udi). La figure finale de ce dernier jeu de ficelle est quant à elle identique à celle de la procédure nebogi (tombée de la nuit - nebogi).
Cette observation est capitale. Elle révèle en effet l’intérêt que les créateurs de jeux de ficelle ont pu porter aux procédures : si l’enjeu avait été uniquement de construire une figure « quatre losange en ligne », ces praticiens n’auraient probablement pas cherché plusieurs procédures menant à des figures de fil exactement identiques.
Nous l’avons vu, l’analyse (ethnomathématique) du corpus trobriandais tend à montrer que la création de nouveaux jeux de ficelle a relevé dans cette région d’un travail intellectuel de choix d’opérations élémentaires et d’organisation de procédures. Cette activité est de nature « géométrique » ou « topologique » en ce sens que les opérations élémentaires et les sous-procédures ont été des outils de travail pour mener des investigations dans des configurations spatiales complexes : investigations confirmées par les transformations d’une figure en une autre, les itérations de sous-procédures, les modifications opératoires, et les chemins différents menant aux mêmes figures ou dessins.
Dans la section suivante, nous allons mettre en perspective cette analyse avec certaines données ethnographiques (autres que les procédures elles-mêmes) relatives à la pratique contemporaine des jeux de ficelle dans les îles Trobriand. Certains comportements récurrents des praticiens de jeux de ficelle, ainsi que l’usage de certains termes vernaculaires, nous informent sur la façon dont des praticiens contemporains perçoivent et conceptualisent cette pratique.
3. Pratique contemporaine des jeux de ficelle trobriandais
3.1 Sens littéral du nom vernaculaire donné aux jeux de ficelle
Dans le village d’Oluvilei, et plus généralement sur l’île de Kiriwina, tous mes interlocuteurs ont fait référence à la pratique des jeux de ficelle en utilisant le terme kaninikula [17]. Selon Linus Digim’Rina, anthropologue de l’université de Papouasie-Nouvelle-Guinée, le sens littéral de kanini pourrait être « éplucher en utilisant les dents », et le terme kula dériverait du verbe kuri que lui-même traduit par l’expression « comment obtenir/gagner » (Digim’Rina, com. personnelle, 2010). Si la traduction de kanini par le verbe « to peel » est également avancée par Senft (1986 : 539), l’étymologie du terme kula demeure une question ouverte. L’anthropologue Johnny Persson affirme quant à lui que kula and kuna (pluie) pourraient avoir la même racine étymologique renvoyant aux notions de richesse et de fertilité (Persson 1999 : 199). Selon ces informations, le sens littéral de kaninikula pourrait donc être « comment obtenir/faire croître/grandir (une figure de ficelle) en épluchant/opérant avec les dents » [18].
Cette interprétation du sens littéral du terme kaninikula suggère donc un lien entre les aspects gestuels de la pratique des jeux de ficelle et les notions de croissance et de fertilité, mais aussi avec l’action d’éplucher des tubercules (Vandendriessche, 2014c). On peut remarquer de plus que l’interprétation de la racine kanini proposée par Digim’Rina s’accorde bien avec le fait que les dents sont très souvent utilisées lors de la réalisation de figures de ficelle, ce qui constitue une particularité de la pratique mélanésienne de cette activité.
Enfin, selon John Kasaipwalova — poète trobriandais, intellectuel qui a une très bonne connaissance des différents dialectes parlés dans les îles Trobriand [19] — le terme kaninikula fait référence à la procédure de jeu de ficelle dans sa globalité, dont la figure produite n’est qu’une étape parmi d’autres [20].
3.2 Aspect procédural des jeux de ficelle
Comme mentionné plus haut, Gunter et Barbara Senft ont mené dans les années 1980 une étude sur les jeux de ficelle pratiqués dans le village de Tauwema de l’île de Kaile’una (voir Fig. 1). Sans chercher à enregistrer les procédures, leur enquête a principalement eu pour objectif la collecte, la traduction et l’analyse des textes oraux (vinavina) qui parfois accompagnent l’exécution d’un jeu de ficelle dans les îles Trobriand (voir section 3.4). Au cours de cette enquête, ils cherchèrent à estimer le degré de connaissance des figures de ficelle par les habitants du village de Tauwema et de ses environs. Dans ce but, ils ont demandé à un groupe d’informateurs de reconnaître et de nommer des figures finales de jeux de ficelle qui avaient préalablement été dessinées par les chercheurs sur une feuille de papier [21]. Ce protocole a mené à une observation inattendue et remarquable : pour retrouver le nom d’une figure — sans utiliser la boucle de ficelle –, certains informateurs ont en effet spontanément mimé les mouvements impliqués dans le jeu de ficelle auquel ils pensaient (Senft et Senft, 1986). Cette information semble indiquer que les praticiens trobriandais perçoivent un jeu de ficelle comme une procédure dont la figure de fil n’est qu’une étape du processus difficilement dissociable de celui-ci.
J’ai pu observer que les praticiens montrent généralement cette figure à l’assistance pendant un temps très court, avant de la « dénouer » de façon systématique pour revenir à la boucle initiale. Ce retour au point de départ apparaît comme une nécessité pour que le jeu soit considéré comme pleinement réalisé. La procédure misima (nom d’une île de la province de Milne Bay) illustre parfaitement ce phénomène. Elle débute par l’extension de la figure finale qui est seulement montrée quelques secondes à l’observateur. Comme le montre l’extrait vidéo suivant, il s’en suit une longue procédure dont le but est de dénouer cet entrelacement complexe, qu’un débutant transforme généralement en un nœud inextricable :
Cette observation semble confirmer que la figure obtenue n’est perçue que comme une étape d’un processus aboutissant au retour à la boucle de fil initiale. Ceci suggère de nouveau que les praticiens trobriandais accordent une importance primordiale à la procédure dans sa globalité. L’aspect procédural des jeux de ficelle est également mis en évidence par le rythme que les praticiens donnent à la réalisation d’une figure de ficelle. Les procédures de jeu de ficelle sont en effet rythmées par une exécution cadencée des opérations. L’exemple de la procédure magiaweda (chauve-souris) montre très distinctement que certains gestes sont accentués par la praticienne — parfois presque exagérément, dans le sens où cette accentuation n’est pas techniquement nécessaire. En particulier, les opérations d’insertion d’un doigt dans une boucle sont très amplifiées. De plus, un court temps d’arrêt est marqué entre chacune des opérations, ce qui a pour effet de séquencer la procédure aux yeux de l’observateur :
3.3 Terminologie vernaculaire associée à la pratique des jeux de ficelle
Des termes vernaculaires sont parfois employés par les praticien(ne)s trobriandais(es) pour désigner des actions exécutées lors de la pratique des jeux de ficelle, dans des situations de transmission d’une personne à une autre, mais de façon non systématique.
Les termes utilisés tendent à indiquer que les notions d’opération élémentaire et de sous-procédure — révélées par l’analyse ethnomathématique du corpus — relèvent d’une certaine perception locale. Dix expressions vernaculaires que j’ai collectées à Oluvilei désignent en effet des actions sur le fil dont la plupart ont été analysées plus haut comme des opérations élémentaires (section 2.1). Par exemple, l’expression kukilova désigne la libération d’une boucle par un doigt. kilova est un verbe que l’on peut traduire par « libérer ». Ainsi ku-kilova signifie « tu libères ». Bien que non spécifique à la pratique des jeux de ficelle, la forme grammaticale ku + verbe est la forme générale des expressions liées à la désignation des opérations dans le contexte de la pratique des jeux de ficelle. Ce dernier point semble révélateur de l’utilisation de cette terminologie dans une situation de transmission à destination d’un individu-apprenant. Le tableau 1 ci-dessous présente cette terminologie. L’existence de ces termes est de fait un indice de ce que les praticien(ne)s trobriandais(es) perçoivent un jeu de ficelle comme étant constitué d’un ensemble de gestes simples correspondant — au moins pour partie — aux opérations « élémentaires » que l’analyse ethnomathématique a pu mettre en évidence.
Tableau 1
| Termes vernaculaires | Traduction française | Opérations élémentaires |
|---|---|---|
| kusui | tu vas à l’intérieur | Insérer (un doigt dans une boucle) |
| kutasuki | tu saisis | Saisir (un fil avec face dorsale du doigt, les dents, ou entre deux doigts ; plusieurs fils à la fois avec la main) |
| kukwau | tu prends | Crocheter vers le haut |
| kutum | tu couvres/dissimules | Crocheter vers le bas |
| kukwaimali | tu reviens | Revenir en position |
| kukilova ou kukilai | tu libères | Libérer (une boucle, un doigt) |
| kukwili | tu tournes | Rotation verticale / rotation horizontale |
| kutaya | tu déposes | … |
| kwatupini | tu torsades/tortilles | Torsader (une boucle) |
| lupulapu | … | |
| … | Tendre (le fil) | |
| … | Passer un doigt au-dessus/en-dessous d’un fil ou d’une boucle |
Les deux dernières expressions lupulapu et kwatupini du tableau 1 ne sont pas — à première vue — sous la forme grammaticale ku + verbe mentionnée plus haut. Dans le cas de l’expression kwatupini, le verbe est en fait katupini (tortiller/tourner/tordre). L’opération est donc indiquée par ku-katupini ; qui, dit rapidement, devient kwatupini (tu tortilles) (Com. pers. Senft, 2013). L’expression kwatupini est donc le résultat de la contraction d’une expression de la forme ku + verbe. Ce n’est pas le cas de l’expression lupulapu qui, à ma connaissance, ne dérive pas de cette forme grammaticale. Par ailleurs, l’usage de ce terme semble spécifique à la pratique des jeux de ficelle (Com. pers. Senft, 2010), contrairement aux autres expressions qui peuvent être employées dans des contextes divers. Lupulapu désigne l’opération qui consiste à saisir un fil entre le pouce et l’index au travers d’une petite boucle :
Cette opération est utilisée et itérée dans la seule procédure budibudi du corpus (budi budi) et se caractérise de ce fait par sa faible occurrence. Je n’ai pas identifié ce geste technique comme une opération élémentaire nécessaire à la description des procédures du corpus. Il est en effet possible de décrire cette opération en invoquant l’opération « attraper un fil entre deux doigts » et en précisant le fil à saisir. Pourtant, cette opération semble mise en exergue tout à la fois par sa forme grammaticale et par son usage spécifique à la pratique des kaninikula, suggérant ainsi qu’elle est perçue par les praticiens comme une opération singulière parmi l’ensemble des gestes impliqués dans la réalisation des figures de ficelle.
Une seconde opération est explicitement nommée par les acteurs, alors que mon analyse proposait de la confondre avec l’une des opérations élémentaires introduites dans la section 2.1. Il s’agit de l’opération nommée kutaya (« tu déposes »). Cette opération consiste à effectuer une rotation horizontale des mains dans le but de déposer sur le sol ou sur les genoux la configuration de fil obtenue à l’issue de l’ « ouverture A » :
Cette opération permet ensuite d’attraper le fil d’une autre façon : voir par exemple le début de la procédure nebogi — nebogi. L’opération kutaya peut être analysée comme une simple rotation horizontale, suivie de la libération des boucles ; libération qui est induite par la rotation (si bien sûr les doigts sont desserrés).
Inversement, j’ai pu relever que les praticien(ne)s de jeux de ficelle trobriandais désignent par un même terme (kutasuki) quatre opérations élémentaires de saisie du fil que mon analyse ethnomathématique proposait de distinguer : « saisir » (le fil) avec la face dorsale du doigt, « pincer » (le fil) avec les dents, « attraper » (le fil) entre deux doigts, « prendre » plusieurs fils à la fois avec plusieurs doigts. Cette observation est un indice de ce que ces quatre opérations sont perçues comme de même nature par les Trobriandais. Il en est de même des rotations verticale et horizontale qui sont décrites par le même terme kukwili (tu tournes).
Aucun terme vernaculaire ne semble employé pour désigner les opérations élémentaires « passer » (par le côté distal / proximal) et « tendre » (le fil). Concernant cette dernière, on peut remarquer que le fil doit être légèrement détendu pour que les opérations puissent être implémentées. Ce relâchement du fil est suivi de façon systématique par la tension du fil, et un court temps d’arrêt est alors marqué. Il est possible que le caractère systématique de cette action de tension confère à cette opération un statut différent des autres opérations élémentaires.
Bien qu’un nombre important de sous-procédures — i.e. séquences d’opérations élémentaires que l’on retrouve à l’identique dans plusieurs jeux de ficelle ou bien qui sont itérées au sein de la même procédure — soient présentes dans le corpus de jeux de ficelle d’Oluvilei, seulement trois d’entre elles sont nommées en Kilivila. Il s’agit des (courtes) sous-procédures kwatuponiniya, kwalili (décrites dans la section 2.3 sous l’appellation « Caroline extension » et « Navaho » respectivement) et sosewa. Lorsque deux boucles ont été « saisies » par le pouce et l’index d’une main, exécuter sosewa revient à « insérer » dans ces deux boucles l’auriculaire et l’index de la main opposée, et à les « transférer » à ces deux mêmes doigts :
Ces trois sous-procédures se caractérisent par le fait qu’elles sont composées d’un petit nombre d’opérations élémentaires et ont une forte récurrence dans le corpus. Par ailleurs, selon mes informateurs, ces termes ne sont employés que dans le contexte de la pratique des jeux de ficelle. L’existence de ces trois termes est d’une grande importance pour l’analyse : cette terminologie — spécifique à cette pratique — est en effet un indice de la reconnaissance par les acteurs d’une suite « ordonnée » d’opérations : les termes kwatuponiniya, kwalili et sosewa font en effet référence à des séries d’actions qui pourraient être décrites en invoquant la terminologie relative aux opérations élémentaires (par exemple kwalili = kutasuki + kukilai), ce sont donc bien des séries ordonnées d’actions (sur le fil) qui ont été identifiées et nommées par les praticiens trobriandais.
Si je n’ai pas encore eu accès au sens littéral des termes kwatuponiniya et kwalili, on peut faire des hypothèses sur le sens de sosewa. Ce terme pourrait être l’équivalent du verbe soseva (recueillir, ramasser, rassembler) noté par Gunter Senft (1986 : 372). Notons, d’une part, que cela décrit parfaitement le geste que désigne le terme sosewa. De plus, la substitution du « v » par le « w » est l’une des différences dialectales entre le Kilivila parlé à Oluvilei et la langue qu’étudie Senft sur l’île de Kaile’una. Par exemple, le jeu de ficelle appelé kapiwa (abeille) à Oluvilei (section 2.1) est nommé kapiva par les habitants du village de Tauwema sur Kaile’una (Senft et Senft, 1986 : 112).
Comme mentionné plus haut, à ma connaissance, les longues sous-procédures ne portent pas de nom dans les îles Trobriand ; là encore, c’est plutôt par le rythme donné aux procédures de jeu de ficelle que les Trobriandais(es) semblent les mettre en évidence ; un rythme parfois soutenu par l’énonciation de textes oraux qui accompagne la réalisation de certains jeux de ficelle dans les îles Trobriand.
Nous l’avons vu, les concepts (ethnomathématiques) d’opération élémentaire et de sous-procédure renvoient à une conceptualisation du processus développée par les acteurs eux-mêmes. Si ces deux outils d’analyse (opérations élémentaires et sous-procédures) correspondent parfois à des termes explicites chez les praticiens trobriandais, les critères autochtones de catégorisation de ces gestes techniques diffèrent dans certains cas significativement de ceux que j’ai précédemment définis, et témoignent de la façon dont ces acteurs perçoivent les opérations à l’œuvre dans les procédures de jeu de ficelle. Cela a été mis en évidence notamment par les quatre opérations élémentaires de saisie désignées par un même terme en Kilivila. Comme je l’ai mentionné plus haut, les termes techniques sont utilisés par les praticiens de jeux de ficelle dans des situations de transmission, et semblent avoir pour premier objectif de souligner certains gestes montrés à l’apprenant. En revanche, je n’ai jamais observé la transmission d’une procédure de jeu de ficelle d’un praticien à un autre par le simple usage de cette terminologie technique, comme cela a pu être noté par exemple dans les îles Tuamotu il y a quelques décennies [22] (Maude et Emory, 1979). Néanmoins, cette possibilité n’est pas exclue chez les Trobriandais, et des recherches futures permettront certainement d’élucider ce point. Si la terminologie autochtone relative à la pratique des kaninikula semble — à première vue — ne pas être suffisamment précise pour décrire (sans manipulation du fil) chaque étape d’un jeu de ficelle, il est possible que certaines informations soient implicites et induites par le contexte : le geste que l’apprenant doit réaliser lorsque l’expression kutasuki (« tu saisis ») est énoncée pourrait être interprété par le praticien en fonction du contexte ; la situation opératoire induirait implicitement laquelle des quatre opérations de saisie doit être réalisée, voire le fil à saisir.
Conclusion
Si depuis la fin du 19ème siècle, certains anthropologues ont perçu l’aspect procédural de la pratique des jeux de ficelle, la relation entre cette activité et les mathématiques n’a été que très peu étudiée au cours du 20ème siècle. Dans la présente étude, nous avons pu mettre en évidence la manifestation d’une forme de rationalité mathématique associée à cette activité : la création des jeux de ficelle trobriandais provient en effet d’un travail intellectuel mobilisant les concepts de procédure, d’opération, de sous-procédure, de transformation et d’itération. Ce travail intellectuel a plus précisément consisté en l’élaboration d’algorithmes fondés sur l’organisation en procédure d’un ensemble d’opérations « géométriques » (ou opérations élémentaires) et sur des investigations à l’intérieur de configurations spatiales parfois d’une grande complexité. Ces investigations sont attestées, nous l’avons vu, par les transformations de figures, les variations opératoires, et les itérations de sous-procédures. L’analyse formelle du corpus montre ainsi que les jeux de ficelle ont constitué, pour des praticiens/créateurs, un cadre propice au développement d’une réflexion de nature mathématique.
Les outils d’analyse introduits dans cet article ont permis d’engager une étude comparative de la pratique des jeux de ficelle sur diverses aires culturelles (Vandendriessche, 2014b). Les premiers résultats de cette étude suggèrent qu’une analyse comparée des modalités de la pratique des jeux de ficelle dans différentes sociétés (de l’Océanie, d’Amérique latine, de l’Arctique canadien) peut mettre en évidence des schèmes opératoires distinctifs, culturellement spécifiques, en matière d’organisation des sous-procédures et des procédures constitutives des figures de ficelle. D’autre part, les jeux de ficelle constituent, dans de nombreuses sociétés, des modes d’organisation et d’expression de certains savoirs, d’ordre mythologique, cosmologique, anatomique, ou rituel. Un enjeu majeur des recherches engagées sur la pratique des jeux de ficelle est donc de mieux saisir comment s’articulent, dans ces différentes sociétés, ces différents types de savoirs et ceux de nature mathématique impliqués dans la création de ces procédures [23].
Un exemple en particulier : certaines données ethnographiques relatives à la pratique des jeux de ficelle dans les îles Trobriand et dans les aires culturelles voisines suggèrent qu’une efficacité rituelle positive, en lien avec la fertilité des jardins, est (ou était) conférée à certains jeux de ficelle — ou à la ficelle ayant été utilisée pour cette activité (Landtman 1914 ; Jenness 1920 ; Senft et Senft, 1986 ; Vandendriessche 2014a). Réaliser des jeux de ficelle, en récitant des paroles spécifiques, semble considéré dans certains cas comme ayant un impact positif sur la croissance des tubercules, ignames et patates douces notamment. Dans le cas des îles Trobriand, cette hypothèse est étayée par l’analyse ethnolinguistique des paroles accompagnant ces jeux de ficelle singuliers (Senft et Senft, 1986). Certains de ces textes comprennent des termes vernaculaires identifiés comme étant caractéristiques des formes linguistiques en usage dans les pratiques magiques associées à la culture des jardins trobriandais (Malinowski, 1935). Dans cette perspective, une piste de recherche prometteuse sera d’étudier l’expression d’interrelations entre les processus techniques/pratiques mathématiques impliqué(e)s dans les jeux de ficelle et le processus vital de croissance des tubercules tel qu’il est conçu par les Trobriandais.
Remerciements
Cet article doit beaucoup aux échanges scientifiques que j’ai eus avec Karine Chemla, Sophie Desrosiers et Céline Petit. Cette recherche n’aurait pas été possible sans le soutien du ministère de la recherche - ACI « Anthropologie des mathématiques » (2005-2009) - et celui de la ville de Paris — Projet « Les jeux de ficelle : aspects culturels et cognitifs d’une pratique à caractère mathématique » (2012-2015) financé dans le cadre du Programme « Emergences » 2011. J’ai pu finaliser cet article grâce à l’invitation du Prof. Dagmar Schäfer et du Max Planck Institut fur Wissenschaftsgeschichte (Berlin). Je souhaite exprimer ici ma gratitude envers le Prof. Schäfer.